Posted on

The physics and psychophysics of musical form – the perception of pitch

Music plays with anticipation – setting up a musical trajectory and then satisfying that expectation or, more interestingly, violating the expectation in ways that make musical “sense” and so build and release tension. But what sets up those expectations and determines which patterns of sound make musical sense? Why do some sounds seem pleasant or consonant and others, disturbing or dissonant? How much of this is “built-in” and represents the structure of the hearing apparatus and auditory nervous system? How does our previous experience, our culture and training help shape these experiences? Are there musical universals that reflect some aesthetic of mathematical beauty or is this simply an “artefact” of perceptual and cognitive process: An evolutionary spandrel as discussed in the previous blog?

A hundred and fifty years or so of auditory and musical psychophysics and more recently, direct imaging of the brain experiencing music, has greatly deepened our understanding of these questions but has yet to provide definitive explanations.

Physical resonance, musical instruments and the harmonic series

From a purely acoustical point of view, music can be described as a collection of sounds arranged vertically (that is concurrently sounding) or longitudinally (over time) – or more often, as a combination of both. There are biological constraints that help shape our perception of those sounds as well as learned (cultural) predispositions. 

Our perception of the vertical arrangement of sounds is constrained and conditioned by the frequency resolution of the auditory system – starting at the inner ear. Joseph Fourier’s book on heat flow (first published in 1822) contained within it the kernel of the idea that any continuous function (e.g. a sound wave) is composed of a series of simple sine waves (partials). One  dominant idea in music perception is that the pitch of a note is largely reflected by the lowest frequency component, the fundamental, (although more on this later) and the differences in timbre between instruments are reflected by differences in the higher frequency components or partials.

Tuned musical instruments rely on the property of physical resonance – that is, the mechanical tendency of an object to vibrate at particular sound frequencies. The resonant frequency is a property of the stiffness of the material (e.g. wood, brass or a stretched hide for instance) and the mass of the object (e.g. a cathedral bell compared to a sleigh bell). With a musical instrument, the player puts energy into the instrument (e.g. by blowing, bowing, plucking or hitting it) which excites its resonant frequency.

Musical instruments are designed so that the player can vary the resonant frequency (e.g. by varying the length of the string or effective tube length) to create a melody. Look inside a piano and you will see the arrangement of many strings systematically varying in thickness (mass), length and tension (stiffness). The hammers connected to the keys, strike the strings and cause them to vibrate at their resonant frequency and the multiple keys enable the vertical arrangement of notes.

Because of the complex mechanical structure of many tuned musical instruments, the emitted sound is not a simple sine wave at the resonance frequency (the fundamental) but a complex series of sine waves (partials) whose amplitudes are in turn shaped by other resonances of the instrument (formants). One particular property of natural resonance is that the frequencies of the partials (“overtones” above the fundamental) are usually at integer multiples of the lowest frequency – this is called the harmonic series.


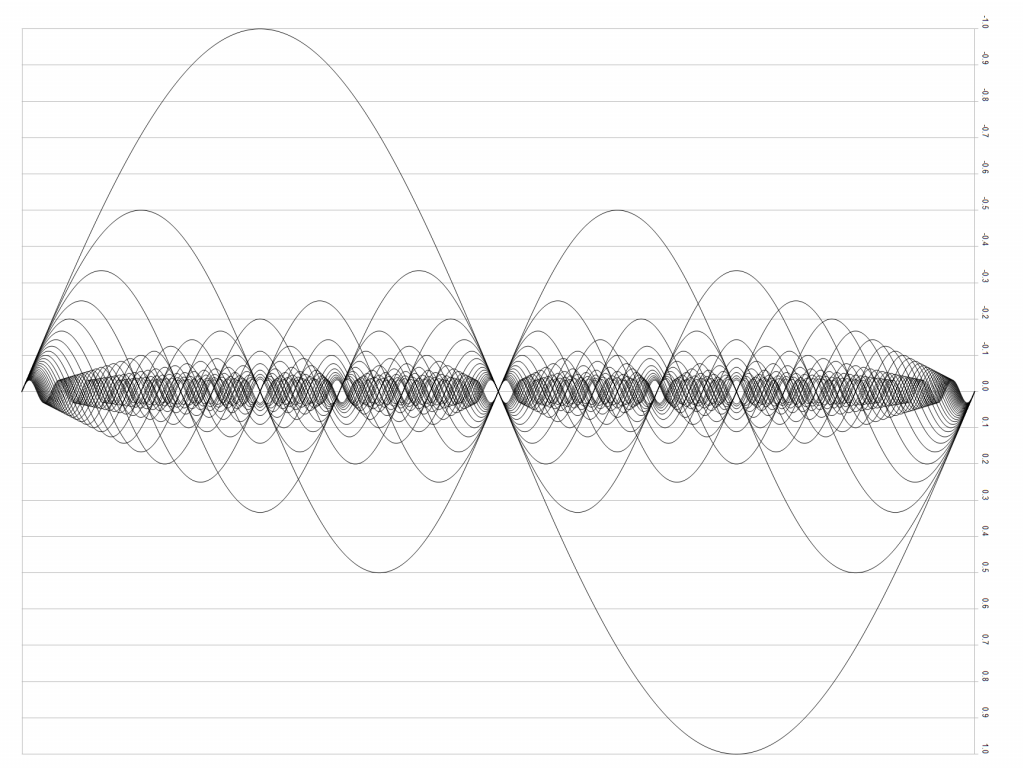
Figure 1: Even numbered string harmonics from the 2nd to 64th harmonic See here

Sound encoding by the inner ear

The inner ear is truly a marvel of biological signal processing. Although smaller than a garden pea, it is capable of encoding sounds over a very wide range of frequencies with wavelengths ranging from around 16 meters to a couple of millimeters! The basilar membrane runs the length of the coiled structure of the cochlea of the inner ear and effectively varies in stiffness and mass over its length. This results in a continuous change in resonance so that different parts of the membrane vibrate at different frequencies – a bit like the arrangement of the piano strings discussed above. 

Figure 2: A sketch of the left ear showing the shape and placement of the coiled cochlea (‘6’)
Figure 3:  The basilar membrane running the entire length of the coiled cochlea

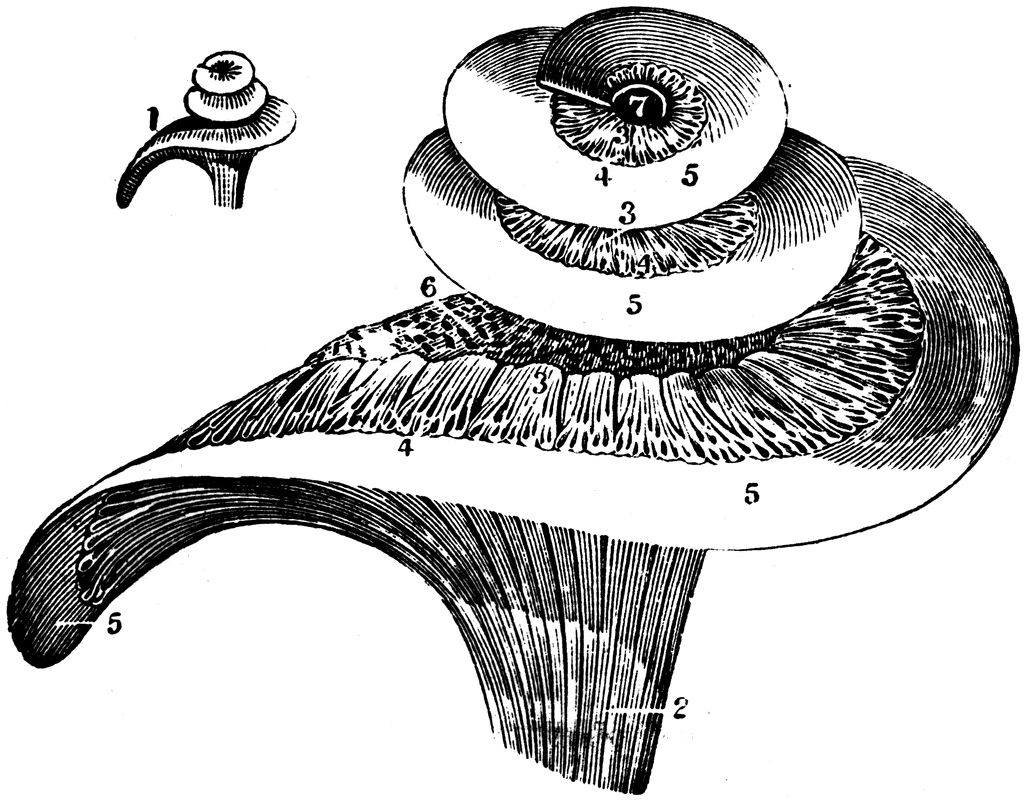
The auditory nervous system is able to detect which parts of the basilar membrane are vibrating, indicating the presence of sound energy at those frequencies. This is often called the ‘place code’ of frequency. Check out Brian Aycock’s take on a quite famous video of the inner ear from Jim Hudspeth’s lab now at the Rockefeller.

Resolution and precision of hearing: Auditory “Critical bands”

While Fourier’s maths focussed on continuous functions, the inner ear (and modern digital signal processing for that matter), necessarily works using discrete steps in frequency. From this account, it is the resolution and precision of the inner ear (we will take accuracy as a given for the moment) that contributes to the perception of consonance and dissonance. For example, if we consider two sine waves far apart in frequency, the inner ear can faithfully represent both (the very high and very low notes in the video demo above). These are referred to as “resolved” partials. If these sound waves are part of the harmonic series then we tend to hear them as consonant. 

If we bring the two sine waves closer together in frequency, however, they will begin to interfere and at some point they could be considered to be within the same auditory information channel and are referred to as “unresolved” partials. When two partials interact in the same channel, it gives rise to rapid fluctuations of the energy in the channel and a “roughness” in the output. Even if they are part of the harmonic series they will tend to be perceived as dissonant (we will dig much more into this very important topic later). The point at which the two sine waves begin to interfere provides an insight into the encoding precision of the inner ear – essentially, the frequency bandwidth of encoding (also known as the auditory “critical band”). Most importantly, the critical bandwidth increases with frequency: that is, for a low center frequency the bandwidth is narrow and for higher frequencies it is much broader. When calculated on a logarithmic scale, however, the bandwidth is fairly constant and represents equal physical distances along the basilar membrane. Of course, if we take two sounds that are each composed of a series of harmonics, the harmonic components themselves will begin to interact at higher frequencies (where the critical bands are wider), even if the fundamentals are resolved. It is these sorts of interactions that give rise to many of the interesting colors in vertical harmony. 

Time – the other code for pitch?

Although the above model of pitch and timbre perception is both elegant and appealing, there are a number of perceptual phenomena that are not well explained! The first is the case of the missing fundamental. Imagine playing a low note on the piano very softly. The physical properties of the outer and middle ear means that we are more sensitive to frequencies in the middle range of our hearing (another story of resonance – but for another day). If we play our piano note softly enough, the energy at the fundamental (lowest) frequency will not be detected by the auditory system but the middle and upper partials will. The curious outcome is that the perceived pitch of the note is still at the fundamental frequency, although we know that there is not enough energy there to be detected! This is the case of the missing fundamental and it suggests that some relationships between the upper partials are involved in producing the perception of pitch. 

Early theories of pitch perception suggested that the auditory brain retained a “template” of the place code of a particular harmonic spectrum associated with a pitch. If the lower harmonics were missing, pitch could still be perceived because of the match of the upper partial to most of the template but maybe the sensation was not as strong. Another obvious clue to pitch is that each partial is at a frequency that is a whole number multiple of the missing fundamental. Possibly, the auditory system is doing some calculations to determine what that number is given the differences in the partials that it can detect – the so-called Greatest Common Divisor (GCC). 

There is however, another more salient feature of the combined waveform that can provide the auditory system a clue – the frequency at which the combined waveform modulates its amplitude over time. For instance, if we add two sine waves at 800 Hz and 900 Hz, the overall waveform modulates in amplitude at 100 Hz. This is illustrated for a more complex waveform in Figure 4.

Figure 4: Top waveform shows a complete series of harmonic components from 100 to 800 Hz while the bottom waveform is missing the bottom two harmonic components. Note that the periodicity of both waveforms is still 100 Hz, representing the harmonic spacing of the components.

One way in which the auditory system could easily measure this periodicity is by autocorrelation – this is where two copies of the signal are combined together with various delays between them. When the delay matches the periodicity of the input there is a maximum in the output of the detector. From the neurological perspective, this is a conceptually simple way in which a neural circuit could carry out such an analysis (first proposed by J C R Licklider back in 1951). A more general and very important aspect of this approach, is that the focus is on the time domain and how things change over time rather than in the frequency domain as viewed through the Fourier-like analysis of the place code. Some of my colleagues from Oxford have some lovely examples of the missing fundamental and pitch perception here.

Despite the relative simplicity and elegance of this model, there are again, a number of observations that are not well explained. Some sounds with a strong autocorrelation peak do not exhibit a strong pitch and some sounds with no autocorrelation peak still exhibit a pitch. A complication here is how to measure pitch salience and some of the modelling points to the need to incorporate more biologically plausible filtering of the inner ear in the explanatory models.  No one has yet demonstrated the simple neural circuit necessary to compute the autocorrelation function but there is some neurophysiological evidence that is consistent with this sort of time domain analysis. Some researchers have developed models that don’t require time shift but rely on the phase differences in different auditory channels.

Complicating our understanding of these phenomena are perceptual differences in the listeners themselves! The missing fundamental of sounds with a small number of harmonics is heard by some people (so called synthetic listeners) but not by others (analytic listeners). A large study of more than 400 listeners (musicians and non-musicians) demonstrated that this perceptual bias is also reflected in brain asymmetry in the processing of pitch: left hemisphere for those who heard the missing fundamental and right hemisphere for those who did not. Interestingly, musicianship did not predispose to one or other of the cortical asymmetries but did correlate with the overall volume of the brain area responsible (Heschel’s gyrus). Of course, that doesn’t tell us if this represents an evolutionary diversity in brain structure or an acquired difference through brain plasticity and experience (learning). It does, however, give us some confidence that the diversity we see in human perception has a neurophysiological basis and does not necessarily represent an incompleteness or total misdirection in our models. This also still leaves open the possibility for other time domain descriptions of musical pitch – the idea of autocorrelation as the basis for pitch perception is a fairly blunt computational instrument and from the psychophysical evidence, is clearly an incomplete explanation.

Recap and next steps

We have covered a lot of ground here – it’s pretty dense and technical – but we have reviewed a lot of the ideas around the physical and perceptual basis for how we judge the pitch of a complex sound. 

The auditory system codes frequencies using a place code of frequency that is based on a progressive change in the stiffness and mass of the basilar membrane in the inner ear. This results in a progressive change in the resonant frequency along the membrane and different regions move in response to the presence of particular sound frequencies entering the ear. The auditory system is able to detect which locations on the membrane are moving and hence the frequencies of the partials in complex sounds. 

There are also time codes of frequency that respond either to the fundamental frequency of a sound or to the amplitude modulation of the overall waveform that results from the addition of the different harmonic components. The problem of the “missing fundamental” provides good evidence that coding strategies other than the “place code” of frequency are probably in operation. The coding of the timing of individual harmonic components in a complex sound and its contribution to the perception of pitch, remains an interesting and largely open question. 

Sounds made by many tuned musical instruments contain components other than the fundamental frequency of the note and these are most often harmonically related as whole number multiples of the fundamental (the harmonic series). The coding precision of the inner ear means that when two sounds are close in frequency they will mutually interfere and this can be used to define the auditory “critical bandwidth” and the precision (bandwidth) of auditory encoding. 

When two sounds are within the same critical band the sounds are referred to as unresolved. This gives rise to a rapid amplitude modulation (or roughness) of the level in the channel and is most often perceived as dissonance. As sounds produced by musical instruments often have complex sets of harmonic components, the upper harmonics of two (or more) sounds whose fundamental frequencies are resolved can interact at higher frequencies as unresolved components. The amount of overlap of harmonics can also be determined by the relationship of the fundamental frequencies of the sounds and how they relate to the harmonic series. This gives rise to the broad range of harmonic colours that musicians and composers can use to build and release tension in their music and take listeners on emotional journeys that evolve over time.

The story is far from complete and there are quite a lot of interesting anomalies between perceptual experience and the explanatory models. In the next blog we will dig a little further into some of these questions. With an understanding of the building blocks of the acoustical physics and the sensory conditioning of auditory encoding, we can also look at how the harmonic series informs the formation of scales and the development of keys and modes. These form the acoustic and perceptual frameworks that we use to create and experience musical stories – from “happy birthday” to the joys of Mozart, the profundities of Beethoven and Mahler and the sublime sounds of jazz. The richness of this language across time and cultures has its basis in these simple principles. 

Posted on

The origins and purpose of music

The evolution of music

We all have a common sense of what music is. But why is it? Evolutionary biologists will tell you that various physical and cognitive capabilities evolved because they confer some adaptive advantage in the struggle for survival: Either prolonging life (finding prey and/or avoiding predators) and/or attracting a mate so that you can pass on genes. The first is referred to as natural selection and the second, sexual selection. The idea is that any advantage that comes from subtle variations in an organism’s genetic makeup is preserved in the species through procreation. Neither of these evolutionary drivers seem to be easily applied to music.

In this blog I want to review some of the main ideas about where music came from and why it has taken on the role(s) that it has in our daily lives. Along the way we will learn a little neuroscience and psychology. And while we are talking about neuroscience, in the next blog I will look more at the cognitive neuroscience and neurochemistry of how and why music affects us emotionally the way it does. But for now, let’s dive in and look deeper at some of the ideas about how and why music developed at all.

Back in the day, Darwin thought that music might be important in sexual selection in the same way that bird song and frog calls are important for those species. There is no question that the brain is to some extent, wired for music – young babies can appreciate musical form with little exposure or instruction and brain lesions at any age can eliminate some (or all) elements of musical capability. Music also appears to have been around for a goodly chunk of the time since the emergence of modern humans (homo sapiens) indicating that it’s probably characteristic of the species. But human music is quite different from the stereotyped calls of other species. By contrast, it’s not fixed in form or function but highly flexible in its characteristics and applications. The huge diversity of modern genres (Spotify identifies 1300) not to mention the range of music over the world’s different cultures and over the ages is obvious testament to that. This flexibility is called intentional transposability and it shares that characteristic with human speech.

From Koonin (2016) Figure 1

The great evolutionary biologist Stephen Jay Gould and his colleague Richard Lewontin argued back in 1979 that not every biological feature needed to arise as a consequence of selection but could arise as a consequence of other features which were selected for – a sort of “get it for free” idea.

They called these things “spandrels” after the shape of two arches meeting in support of a dome in Byzantine and Renaissance church architecture – while spandrels add to the overall aesthetic of the building they simply arose out of the geometric necessity of the architectural plan. Not everyone has adopted the term but the idea persists and is also referred to as exaptation and many examples  have been described (like feathers for warmth being deployed for flight etc.). I have very fond memories of sitting in a packed auditorium in the middle of a Sydney summer (without air conditioning) listening to Gould lecture on this – he was an amazing scientific orator!

So maybe music is a spandrel/exaptation and we enjoy this amazing faculty as a consequence of the development of other cognitive and brain functions. But before we take that tack, let’s look at some of the work that has been done about how music could convey an advantage to the species, if not directly to the individual organism! 

Social and cultural context

Contemporary evolutionary biology is often seen in terms of the selfish gene (to use Richard Dawkins’ term) and about the survival of the individual organism in an environment that is “red in tooth and claw”. But this is not necessarily the most accurate or even a useful account of the human organism. Humans are a highly social species. Like other hominids (gorillas and chimpanzees etc.), humans live in groups and practice a range of behaviors that contribute to group cohesion. While it has been a long time since we have ritually picked the lice and nits off our neighbor to make them like us, Robin Dunbar (1996) has argued that, as hominid groups became larger, physical grooming was increasingly less practical. One solution would have been to connect using sound – a sort of vocal grooming. While early vocalization may have contributed to group harmony, the sounds themselves were probably not terribly meaningful in a semantic or symbolic sense. But this might have been a pressure for the selection of vocal capability. On this theme, David Huron (2001) argues that, from the available evidence, this points to a plausible origin for music (and speech) – a point that is reprised in his book “Sweet anticipation (2006)”.

There are strong reasons why humans favor group living – human babies are born very immature compared to many other species – i.e. they are altricial and require a long period of nurturing and protection if they are to mature to where they are able to pass on genes. The strength of bonding between the child and mother and other carers is critical to that survival. It takes a village to raise a child (or at least an extended family to raise many children) so the neurochemistry of bonding is firmly established in the human brain – Dopamine, Oxytocin, Serotonin and Endorphins. We will look at these in the context of music and emotion in more detail in the next blog but suffice to say here that many different human social interactions promote the release of these neurotransmitters. On release, neurotransmitters promote, among other things, pleasure, trust and other predispositions that enhance group bonding. So even before humans started to band together into larger groups, it is very likely that the bonding neurochemistry was strong. Of course, the brain was continuing to evolve (slowly) as was the vocal apparatus and its neural control systems, so it is likely that the range and capability of vocalization was evolving as well under the selective pressure of vocal grooming. Better vocal grooming could lead to larger cohesive groups which on balance, increased the individual’s chance of maturing and surviving.

Oxytocin – one of the neurochemicals important in human bonding is release deep in the brain form the posterior pituitary organ – From Quintana and Guastella 2020

Music, speech and the Theory of Mind

Clearly at some point in this evolution, music and speech took slightly different development paths but there are myriad studies of the cross linkages between these two functions – Aniruddh Patel provides a very detailed analysis of many of those connections in his book Music Language and the Brain (2010). One thing that is very clear, is that over the roughly 200 thousand years these capacities developed, it is extremely unlikely that this development occurred as a consequence of the accretion of many small genetic changes. Something big happened that produced a profound leap forward in the capacity of the human brain. Although the details are still not clear, at some point the human brain developed a sophisticated capacity that is referred to as Theory of Mind (ToM). Essentially, this is the capacity to recognize and analyze the mental and emotional state of others and to use that to interpret and predict their behavior. Over the last 2-3 decades, we have learned a lot about the emergence of ToM in the developing human from infant to adulthood. One powerful characteristic is the increasing capacity for abstraction and the manipulation of symbols that reflect aspects of the world and behaviors in it. Many have argued that this is a strong driver of language development and the development of higher order models of the world.

The neural structures of the Mentalizing Network that is responsible for the Theory of Mind capability in humans – Figure 1 from Monicelli et al 2021

While it is very difficult to get a good understanding of human evolution over a couple of hundred thousand years, what we can say is that over that period there was an explosion of technical (advanced tools and buildings) and social (symbolic art) and cultural (social and religious organization) phenomena. It is inconceivable, in evolutionary terms, that these could be driven by the accretionary change in genes producing various mental modules that then enabled each of these developments – 200 thousand years is just a blink in evolutionary time! Whether ToM appeared de novo or is related to some more primitive precursor of the mammalian brain, is the subject of much research. The related brain areas have been dubbed the mentalizing network (see figure and review above) and located in the higher cortical areas characteristic of the hominids. With the maturation of ToM capabilities in humans, the brain created a cultural “ratchet” such that the success and discoveries of previous generations could be built upon by subsequent generations – firstly through oral and performed traditions and then with the invention of writing – recorded knowledge. Thus human cultural and intellectual development leaped ahead at a pace orders of magnitude greater than evolutionary development. 

Connecting one mind to another

But what has this to do with music? Did it just come along for the ride or, as suggested above, were there other drivers that shaped the development of this faculty. In the human infant, as ToM matures, babies begin to understand that there are other minds out there – shared attention and mimicry, then vocal babbling and interactive play all begin to provide clues. Language is about connecting one mind to another mind and the emergence of common understanding through conversational interaction. The semantic elements in language convey information about object states and interactions which are  important building blocks in decision making. But conversation is also about the non-verbal (multimodal) information made available through posture, facial expression, prosody, gaze etc. The signals passing between minds go well beyond the semantic information and include the affective or emotional context of the communication. This is important for two reasons. Firstly, conversation involves decision making and action (how to respond in the next conversation turn) and all decision making requires the engagement of emotional structures deep in the brain. Secondly, this stream of affective information also helps disambiguate the semantic stream by providing clues to the affective state of the conversant(s). 

What this tells us is that “language” is actually a multimodal stream of information that conveys both semantic information and affective information. But there are other behaviours and capabilities that can also encode that affective information – the arts! In poetry and prose, spoken or written language is used principally for emotional impact but with music, dance, painting etc it is the multimodal and non-verbal aspects of the artefact that convey the affective information. That music can have a powerful emotional impact is indisputable from our own common experience and the growing body of neuroscientific knowledge documenting how the brain reacts to music. Music can convey the intimate emotions of the composer or the performer and shape the emotions of the listener or it might just predispose the listener to see the world around them in a particular way. Music also has the advantage that it can reach very large numbers of people simultaneously. Taking a cue from the idea of vocal grooming discussed above, music is eminently suitable for cultural and social events that involve the group. Music is used in social contexts to increase bonding, to orient the group to particular predispositions (music makes you braver), to provide collective relief or expression (such as grieving a loss). 

From this perspective, as Bill Thompson and Steven Livingstone (2010) have observed, “music is merely one example of a broader biological function of affective engagement”. That is not to undersell the importance and impact of music but rather to contextualize it in a broader understanding of its significance for the brain and for society and culture. The development of ToM not only provided the insight that there are other minds like our own out there but also the capacity to abstract and create symbols that help understand what is going on out there. Musical instruments, musical forms, musical notation, musical recordings all added to the cultural ratchet that then set us on our musical journey. At this point in human history, as consumers and as creators, we are in the emotional embrace of many giants and, with the evolution of musical technologies over the last few decades, it is with sweet anticipation that we look towards tomorrow.